벡터의 직교성과 직선투영

Orthogonality

이번 포스팅에서는 생소한 단어를 접해 볼 것이다. 처음 들으면 생소하지만 뜻을 알게 된다면 입에 착착 감기면서, “직교한다”를 표현할 때 이 단어를 주로 쓰게 될 것이다.

벌써 언급했지만, 선형대수에서 Orthogonality는 Vector 또는 Vector Space가 서로 수직임을 뜻한다.

Orthogonality vectors & Subspace

Why orthogonality vector?

우리는 왜 직교 벡터를 논하는가? 그 이유는 항상 언급해왔듯이 두가지와 관련이 있다.

• Independent basis (벡터가 서로 수직이면 linearly independent하다)
• Easy calculation in linear combination

이 두가지의 특징과 장점 때문에 직교하는 벡터를 찾아야한다.

length of vector $|X|$

x-y 축으로 이루어진 2차원 평면을 생각해보자. x축을 벡터 공간으로 하는 벡터 X가 있다면 벡터 X의 Transpose는 y축 상의 벡터가 될 것이다. $X$와 $X^T$는 수직하며 이 두 벡터의 길이를 구하면, \(\begin{aligned} |X|^2\ =\ X^TX\ =\ \sum_{i=1}^{n} x_i^{2} \end{aligned}\) 가 된다. 또한 이를 그래프로 나타낸다면 유명한 수학 공식이 떠오를 것이다.

By Pythagoras Theorem,

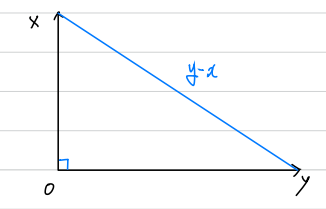
\[\begin{aligned} |y-X|^2\ &=\ |X|^2\ +\ |y|^2 \\ |y-X|^2\ &=\ (y-X)^T(y-X)\ =\ X^TX +\ y^Ty\\ &\Rightarrow y^Ty\ -\ y^TX\ -\ X^Ty +\ X^Ty\ =\ X^TX\ +\ y^Ty\\ &\Rightarrow X^Ty\ =\ 0 \end{aligned}\]

for vector inner product $X^Ty$

1. $X^Ty$ = 0 \rightarrow angle = 90 deg
2. $X^Ty$ < 0 \rightarrow angle > 90 deg
3. $X^Ty$ > 0 \rightarrow angle < 90 deg